
The Traffic Accident Reconstruction Origin -Article-


The Traffic Accident Reconstruction Origin -Article-
|

|
A Three-Point Airborne Trajectory Analysis: An Application of the Derivative
Andrew S. Rich
Introduction
Estimating the take off angle for use in an airborne speed analysis is one of the more challenging problems a reconstructionist can face. Many times, determining this angle from scene evidence is not possible. More typically, a reconstructionist can determine only two points of the vehicle's trajectory: take off and landing. In these cases, the analyst must assume the angle that will result in the most conservative speed estimate. The resulting minimum speed estimate can yield results that are significantly less that the actual speed.
Although rare, scene evidence may offer a third point in the airborne trajectory. The method offered in this paper applies to those circumstances. Knowing this third point precludes an assumption about the take off angle and results in speed estimates of a fine tolerance.
This paper also presents some mathematical concepts that may be of use to the reconstructionist. These concepts include determining a displacement equation for an airborne trajectory, and an introduction to the differential calculus. It is assumed that the reader has a basic knowledge of trigonometry.
Second-degree and Systems of equations
The second-degree equation that is most familiar to a reconstructionist
is a quadratic. The standard form of such a second-degree equation is
![]() . In this form, A, B, and C are constants
(or non-variable coefficients), and
. In this form, A, B, and C are constants
(or non-variable coefficients), and ![]() is the
independent variable. When graphed, this equation describes a parabola. Parabolas occur
frequently in nature and are important to the reconstructionist. When air resistance is
ignored, parabolas describe the trajectory of a bullet, an artillery shell, or an airborne
vehicle. In fact, the study of airborne trajectories is essentially the study of parabolas.
is the
independent variable. When graphed, this equation describes a parabola. Parabolas occur
frequently in nature and are important to the reconstructionist. When air resistance is
ignored, parabolas describe the trajectory of a bullet, an artillery shell, or an airborne
vehicle. In fact, the study of airborne trajectories is essentially the study of parabolas.
For the sake of illustration we will choose a second degree equation where
A=-1, B=8, and C=0.
![]() . This equation,
. This equation,
![]() [A]
[A]
describes a unique parabola and is graphed in Figure 1.
Figure 1
Looking at Equation A, we see that y takes on the following values at specific values of x.
|
When x equals |
y equals |
|
0 |
8 |
|
1 |
7 |
|
2 |
4 |
Table 1
In this case, we knew the equation and then determined three points on the graph. The idea presented in this analysis is to reverse that process. That is, determine the points on the graph, and then write the equation. This is the central concept behind this paper.
We will illustrate the idea by finding Equation A, based on the points in Table 1. First,
we must assume that these points describe a parabola. This is a good assumption as all
equations of this type describe parabolas. We can then say that this parabola can be
described by the standard form ![]() . Next we
take the three points from Table 1 and substitute them into the standard form. This
will leave us with three equations:
. Next we
take the three points from Table 1 and substitute them into the standard form. This
will leave us with three equations:
![]() [1]
[1]
![]() [2]
[2]
![]() [3]
[3]
These three equations contain three unknown coefficients (A, B, and C). Because we have three unknowns and three equations, we can solve for the unknowns by using a system of equations solution. If we look at Equation [1] we see that this is easily solved for C, because A and B are both multiplied by zero. This leaves us with C=8. We will now rewrite Equations [2] and [3] with our value for C substituted.
![]() [2]
[2]
![]() [3]
[3]
We now have two unknown values (A and B) and two equations. Before proceeding, we rewrite both equations:
![]() [2]
[2]
![]() [3]
[3]
We will use what is known as the elimination method in order to solve this system of
equations. Our objective by using the elimination method is to add both equations together,
so that the sum contains only one unknown variable. If we multiply both sides of Equation [2]
by �2, we will be able to eliminate the B variable. When we carry out this multiplication,
Equation [2] looks like this: ![]() . Our two equations
now appear as follows:
. Our two equations
now appear as follows:
![]() [2]
[2]
![]() [3]
[3]
Adding the two equations produces:
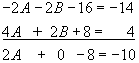 [4]
[4]
We now have an equation that we can solve. Solving Equation [4] tells us that
![]() . We now use this value of A in either Equation
2 or 3 to solve for B. We will arbitrarily choose Equation[2], and substitute �1 for A.
Doing so yields
. We now use this value of A in either Equation
2 or 3 to solve for B. We will arbitrarily choose Equation[2], and substitute �1 for A.
Doing so yields ![]() . Solving for B tells us that
B=0. We now substitute our A, B, and C values into the standard second-degree form, which
yields
. Solving for B tells us that
B=0. We now substitute our A, B, and C values into the standard second-degree form, which
yields ![]() . This should look familiar: It is equation
A, the equation we used to complete Table 1.
. This should look familiar: It is equation
A, the equation we used to complete Table 1.
We can conclude from this analysis that providing we know three points on a parabola, we can determine the unique equation for that parabola. Coupled with the previous observation that all freely falling bodies move in parabolic trajectories, we can also observe that if we can determine three points in an airborne trajectory we can find the equation for that unique trajectory. Next, we will discuss some concepts necessary to better understand this process.
The Derivative
We should all be familiar with the term slope, at least when it applies to a straight line. The slope of a line tells us how much the line rises or falls for each unit of horizontal displacement. We examine this concept by referring to Figure 2.
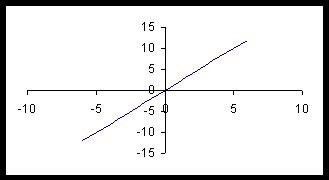
Figure 2
Let's take some points from this graph and present them in a Table.
|
When x equals |
y equals |
|
0 |
0 |
|
1 |
2 |
|
3 |
6 |
Table 2
Looking at Figure 2, we see that for every time our x value increases by 1 unit, the y value increases by 2 units. For example, if we start at the point (0,0) and move to the point (1,2), we see that we moved over 1 unit and up two units. For this graph, we say that the slope is 2.
We do not have to draw a graph in order to determine the slope; we can calculate it
mathematically. We can do this with the equation ![]() ,
which is read, the change in y divided by the change in x. This equation may also be written
,
which is read, the change in y divided by the change in x. This equation may also be written
![]() . To calculate the slope of a line using this
equation, we pick any two points that exist on this curve (a straight line can be a curve)
and substitute them into the slope equation. For this example, we will use the points (0,0)
and (1,2). Substituting these points into the slope equation and solving yields
. To calculate the slope of a line using this
equation, we pick any two points that exist on this curve (a straight line can be a curve)
and substitute them into the slope equation. For this example, we will use the points (0,0)
and (1,2). Substituting these points into the slope equation and solving yields
![]() . This result agrees with what our visual
examination of Figure 2 told us about the slope of the line. In this case, we used the
point (0,0) for our
. This result agrees with what our visual
examination of Figure 2 told us about the slope of the line. In this case, we used the
point (0,0) for our ![]() point. We could have just
as easily chosen the point (2,1), or any other point on the graph, for
point. We could have just
as easily chosen the point (2,1), or any other point on the graph, for
![]() . This is true because the line has the same
slope everywhere along its length. It should be noted that the letter
. This is true because the line has the same
slope everywhere along its length. It should be noted that the letter
![]() is used to represent slope.
is used to represent slope.
Now for the challenge: how do we determine the slope of the graph described by a curved line, such as the graph in Figure 1? At first glance, this may seem impossible. The fact is, the curve doesn't have a single slope, but infinitely many. The slope is constantly changing.
This problem notwithstanding, we can still find the slope of the curve at any particular
point. Let's say we were interested in the slope of
![]() when
when ![]() .
We can visualize what the slope at this point looks like by drawing a tangent line at the
point (1,7). This is shown in Figure 3.
.
We can visualize what the slope at this point looks like by drawing a tangent line at the
point (1,7). This is shown in Figure 3.
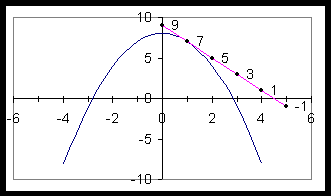
Figure 3
If we could find the slope of this line, we would then know the slope of the curved
line at the point ![]() , because they are the same.
The problem is we only know one point of the straight line, so we cannot calculate the slope
using the slope equation. However, when combined with a limit, the slope equation can help us
determine the slope of a curved line at a particular point. The definition of a limit can be
quite involved. For the purpose of examining airborne trajectories in this paper, we will
define a limit as the value of an equation when a variable in that equation approaches a
certain value. We will use the equation
, because they are the same.
The problem is we only know one point of the straight line, so we cannot calculate the slope
using the slope equation. However, when combined with a limit, the slope equation can help us
determine the slope of a curved line at a particular point. The definition of a limit can be
quite involved. For the purpose of examining airborne trajectories in this paper, we will
define a limit as the value of an equation when a variable in that equation approaches a
certain value. We will use the equation ![]() to
demonstrate the limit. What would be the result of this equation if we let x approach
zero?
to
demonstrate the limit. What would be the result of this equation if we let x approach
zero?
Looking at the graph of Figure 3, we see that as x gets closer and closer to 0, y gets closer and closer to 8. (Note that it does not matter if we approach 0 from the left or the right; either way, the value of y still approaches 8. A thorough study of limits will reveal that this is one of the conditions for the existence of a limit. That is, if we approach zero, in this example, from the left and the right, and y approaches two different values, then the limit would not exist).
In this example, the limit as x approaches 0 for the equation
![]() is 8. In mathematics, we write this as
is 8. In mathematics, we write this as
![]() . We do not need to look at a graph to
determine what the limit of an equation is at a particular point. For many equations,
but not all, all we need to do is substitute the value that x is approaching into the
equation and solve. Here are some examples:
. We do not need to look at a graph to
determine what the limit of an equation is at a particular point. For many equations,
but not all, all we need to do is substitute the value that x is approaching into the
equation and solve. Here are some examples:
![]()
![]()
![]()
We now bring the equation of the slope of a line and the limit concept together in order to calculate the slope of a curved line at a particular point. We will use Figure 4 to help us.
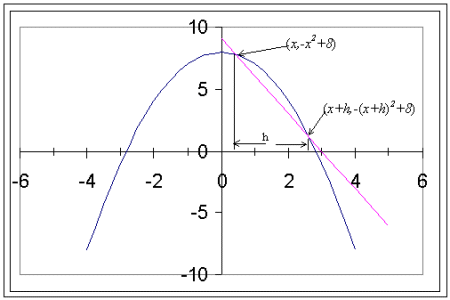
Figure 4
We begin by deriving a general solution to the slope of the secant line (A secant
line is a line that intersects a curve in two places) that intersects the parabola. We
will use the equation for the slope of a line and the points
![]() and
and ![]() .
We also need to recall that the equation of this graph is
.
We also need to recall that the equation of this graph is
![]() . Knowing the equation, we can rewrite the two
points of intersection as
. Knowing the equation, we can rewrite the two
points of intersection as ![]() and
and
![]() . While this may seem complicated, all we did
was substitute the equation of the graph for the y values at the point
. While this may seem complicated, all we did
was substitute the equation of the graph for the y values at the point
![]() and
and ![]() .
Now we use these two points in the slope equation.
.
Now we use these two points in the slope equation.
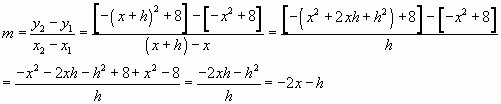
This tells us the equation for a secant line of the graph
![]() is
is ![]() .
However, we are not interested in a secant line; we want to know the slope of a tangent
line to the graph of
.
However, we are not interested in a secant line; we want to know the slope of a tangent
line to the graph of ![]() . To do this, imagine that
h in Figure 4 gets smaller and smaller. As h gets closer and closer to 0, the secant line
gets closer and closer to becoming the tangent line. In fact, when h is 0, the secant line
is the tangent line depicted in Figure 3. With this knowledge, we will use the equation for
the secant line, and use our knowledge of limits to get the equation for the tangent line.
Thus, we can write
. To do this, imagine that
h in Figure 4 gets smaller and smaller. As h gets closer and closer to 0, the secant line
gets closer and closer to becoming the tangent line. In fact, when h is 0, the secant line
is the tangent line depicted in Figure 3. With this knowledge, we will use the equation for
the secant line, and use our knowledge of limits to get the equation for the tangent line.
Thus, we can write ![]() . This tells us that the
equation for the tangent line, at a point x, for the graph of
. This tells us that the
equation for the tangent line, at a point x, for the graph of
![]() is
is ![]() .
.
Recall that we started this section with the intent of determining the slope of the tangent
line when ![]() . Substituting 1 for x into
. Substituting 1 for x into
![]() yields �2. This tells us that the slope of the
tangent line of the graph
yields �2. This tells us that the slope of the
tangent line of the graph ![]() , when
, when
![]() is �2.
is �2.
The concept just introduced is known in the calculus as the derivative. As shown, the geometric interpretation of the derivative is the slope of a tangent line. There are other ways that the derivative can be interpreted, but the geometric interpretation is the one we are interested in for the purpose of this paper.
There are several symbols used to represent the derivative. Two of the more widely
used ones are ![]() (read
(read
![]() prime) and
prime) and
![]() . Thus, we can write: when
. Thus, we can write: when
![]() then
then ![]() ; or when
; or when ![]() then
then
![]() Another way to show the derivative is to substitute
the equation for y into the
Another way to show the derivative is to substitute
the equation for y into the ![]() notation. This gives us
notation. This gives us
![]() .
.
Calculating an Angle from a Derivative
There will come a time in this analysis when we will be interested in the angle that a tangent line makes with the x-axis. If we recall that the tangent of an angle is the sine of the angle divided by the cosine of the angle, or in terms of the figures in this paper, rise divided by run. As we know, rise divided by run is also known as the slope. Thus, if we know the slope of a line, we should be able to calculate the angle it makes with the x-axis by using the inverse tangent function.
In the example above, we found that the derivative of the equation
![]() is
is ![]() .
When
.
When ![]() , the slope of the tangent line is �2. Using
a calculator with trig functions, we find that the angle that has �2 as its tangent is �63.4�.
The minus sign tells us that the angle is being measured clockwise from the x-axis.
, the slope of the tangent line is �2. Using
a calculator with trig functions, we find that the angle that has �2 as its tangent is �63.4�.
The minus sign tells us that the angle is being measured clockwise from the x-axis.
The Power Rule: A Simple Alternative
The approach presented above to determining a derivative by a limit was
rigorous. Fortunately, there is an easier way. Someone noticed a pattern and gave us what
is known as the power rule. Symbolically, the power rule says that for an equation
![]() , then
, then ![]() , where c is a constant (such as �5 in
, where c is a constant (such as �5 in![]() ). Here,
x is the variable we are differentiating with respect to, and n is the exponent
of x. In English, the power rule says that to find the derivative of an equation in the
general form of
). Here,
x is the variable we are differentiating with respect to, and n is the exponent
of x. In English, the power rule says that to find the derivative of an equation in the
general form of ![]() , we multiply the constant by the
exponent, and then reduce the exponent by 1. Here are some examples to help the reader see
this pattern:
, we multiply the constant by the
exponent, and then reduce the exponent by 1. Here are some examples to help the reader see
this pattern:
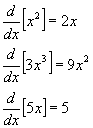
In the last example, the exponent of x is 1. Subtracting 1 from 1 leaves 0 as the new
exponent of x, and anything to the 0 power is 1 (except 0). We also need to know that the
derivative of a constant is 0. For example ![]() .
This is presented without proof, however, the reader is reminded that a line of a constant
equation is horizontal, and a horizontal line has 0 slope. The sum rule will also be helpful
to us. This rule tells us that to find the derivative of an equation that has more than one
term, we find the derivative of each term and add them together. For example, find the
derivative of
.
This is presented without proof, however, the reader is reminded that a line of a constant
equation is horizontal, and a horizontal line has 0 slope. The sum rule will also be helpful
to us. This rule tells us that to find the derivative of an equation that has more than one
term, we find the derivative of each term and add them together. For example, find the
derivative of ![]() . Solution using the power and
sum rules:
. Solution using the power and
sum rules: ![]() . Notice that all we did is take
the derivative of each term of the equation and then add them together. Recall that
. Notice that all we did is take
the derivative of each term of the equation and then add them together. Recall that
![]() . It is a constant and does not affect the
derivative.
. It is a constant and does not affect the
derivative.
An Application to Collision Reconstruction
Let's see how this method would be applied in a real-life situation. We have a car that leaves a two-lane highway, strikes and vaults over a guiderail end-treatment. The vehicle is now airborne over a median, which is 40 feet lower than the roadway surface. During its trajectory, the vehicle strikes and breaks a small tree branch. The vehicle finally comes to rest on the median. This is a circumstance appropriate for this treatment.
When we begin this reconstruction, we need the coordinates for the vehicle's center of mass (COM) at three different locations during its airborne trajectory. In this case, as in most, we know the spot where the vehicle vaulted and where it landed. Recall we also have the additional location given by the tree strike. (Although not discussed in this paper, the reconstructionist needs to consider the pitch of the vehicle when determining the COM positions. We will assume that the measurements presented here are the actual�or very close�positions of the vehicle's center of mass.)
In order to make the math simpler, we consider the point where the vehicle vaulted
as our origin, or the point ![]() . The reader
should realize that these coordinates are called x and y. The convention used in this
paper orients y in a vertical direction rather than the
more customarily used x and y coordinates that lie in the plane of the road.
The other two airborne measurements will be related to the points along the airborne
trajectory. We find that at the time the vehicle struck the branch, the vehicle's COM
had traveled 130.00 feet horizontally and fell 13.30 feet. We will call this point
. The reader
should realize that these coordinates are called x and y. The convention used in this
paper orients y in a vertical direction rather than the
more customarily used x and y coordinates that lie in the plane of the road.
The other two airborne measurements will be related to the points along the airborne
trajectory. We find that at the time the vehicle struck the branch, the vehicle's COM
had traveled 130.00 feet horizontally and fell 13.30 feet. We will call this point
![]() . The COM landed a horizontal distance
of 184.00 feet from its vault point and fell a total distance of 40.00 feet. We
consider this point
. The COM landed a horizontal distance
of 184.00 feet from its vault point and fell a total distance of 40.00 feet. We
consider this point ![]() . We construct a
Table, as we did before, for our three points.
. We construct a
Table, as we did before, for our three points.
|
When x equals |
Y equals |
|
0.00 |
0.00 |
|
130.00 |
-13.00 |
|
184.00 |
-40.00 |
Because an airborne vehicle's path is a parabola, we use these three points to write three different second-degree equations:
![]() [1-1]
[1-1]
By choosing our first point as ![]() , the
A and B coefficients are eliminated from this equation leaving us with C=0.
, the
A and B coefficients are eliminated from this equation leaving us with C=0.
The other two equations are (remember that we found
![]() , therefore the
, therefore the ![]() coefficient does not appear in Equations [1-2] or[1-3]):
coefficient does not appear in Equations [1-2] or[1-3]):
![]() [1-2]
[1-2]
![]() [1-3]
[1-3]
Let's choose to solve this system of equations by eliminating the
![]() coefficient. We can eliminate the
coefficient. We can eliminate the
![]() coefficient if we preferred, but in this case,
the
coefficient if we preferred, but in this case,
the ![]() coefficients are smaller (working with smaller
numbers reduces the chance for errors). The quickest way to eliminate the B
coefficient is to multiply Equation [1-2] by Equation[1-3]'s B coefficient, and
multiply Equation [1-3] by Equation[1-2]'s
coefficients are smaller (working with smaller
numbers reduces the chance for errors). The quickest way to eliminate the B
coefficient is to multiply Equation [1-2] by Equation[1-3]'s B coefficient, and
multiply Equation [1-3] by Equation[1-2]'s ![]() coefficient. In addition, in order for the
coefficient. In addition, in order for the ![]() term to drop out of the final equation, one of the new
term to drop out of the final equation, one of the new
![]() coefficients has to be negative. Therefore, we
can multiply Equation [1-2] by �184 and Equation [1-3] by 130.
coefficients has to be negative. Therefore, we
can multiply Equation [1-2] by �184 and Equation [1-3] by 130.
![]() [1-4]
[1-4]
![]() [1-5]
[1-5]
Now add Equations [1-4] and[1-5]:
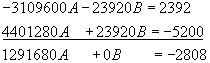 [1-6]
[1-6]
Solving Equation [1-6] for A yields ![]() 174.
We can now substitute our known value for A into one of the original Equations ([1-2]
or [1-3]), and then solve for B.
174.
We can now substitute our known value for A into one of the original Equations ([1-2]
or [1-3]), and then solve for B.
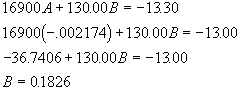
Now that we know our A, B and C coefficients, we can write the equation for the height of the vehicle, as a function of the vehicle's horizontal displacement:
![]() [1-7]
[1-7]
Where h is the height (in feet) of the COM and x is the horizontal displacement of the COM.
Now let's prepare to find the angle that the vehicle vaulted. We take the derivative of Equation [1-7] using the power and sum rules:
![]() [1-8]
[1-8]
Equation [1-8] will give us the slope of a tangent line at any point along the vehicle's
trajectory. In this case, we are interested in the tangent line when the vehicle first vaults,
or when ![]() . Substituting 0 for x into Equation
[1-8] tells us that the slope of the tangent line at this point is 0.1826. Now we take the
inverse tangent of 0.1826, which tells us the vehicle went airborne at 10.35�.
. Substituting 0 for x into Equation
[1-8] tells us that the slope of the tangent line at this point is 0.1826. Now we take the
inverse tangent of 0.1826, which tells us the vehicle went airborne at 10.35�.
We now have enough information to use a standard airborne equation. Instead, let's take this analysis one step further. We will not use a derived equation to determine the vehicle's speed when it vaulted. Instead, we will use some general ideas of airborne trajectory analysis. Those ideas are:
1) The time spent falling equals the time spent traveling horizontally.
2) When the vehicle is at the highest point in its trajectory the tangent line will be horizontal.
We know that when the vehicle is at the highest point in its trajectory, its apex, the tangent line to the trajectory will be horizontal. Since a horizontal line has 0 slope, we will set Equation [1-8], the equation for the derivative, equal to 0 and then solve for x. This will tell us how much distance the vehicle traveled horizontally when it reached the apex.
![]()
We can now take this value and plug it into the height equation (Equation [1-7]):
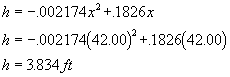
Because we are only concerned with what the car is doing vertically, we know that the
vehicle rises a distance of 3.834 feet to the apex, where the vertical velocity is
instantaneously 0 fps. We also know the vehicle acceleration in the vertical direction is
always 32.2 ft/sec2, or the acceleration of gravity. Therefore, we can use
![]() to calculate the vehicle's initial vertical
velocity.
to calculate the vehicle's initial vertical
velocity.
![]()
Next, we can calculate the time required for the car to rise to its apex:
![]()
Now, we need to calculate the time it takes the vehicle to fall from its apex, to the point where it hits the ground. We know that the vehicle lands 40.00 feet below its vault point. We also know that the vehicle rises 3.834 feet after vaulting. We can add these two distances together to find how far the vehicle falls from apex to where it first hit the ground.
![]()
We calculate the time it takes the vehicle to fall from apex to where it first hit the ground:
![]()
Now we add this time to the time it took for the vehicle to rise to its apex:
![]()
Thus, the vehicle was airborne for a total of 2.138 seconds. This time is the same time the vehicle was traveling horizontally. Knowing this time, and the distance the vehicle traveled horizontally, we can calculate the vehicle's horizontal velocity:
![]()
We now must calculate the resultant of the vertical and horizontal components of the vehicle's speed, at the time it vaulted, in order to know the speed the vehicle was traveling when it vaulted:
![]() or 59.65 mph.
or 59.65 mph.
Of course, someone has derived an equation that we can plug our two distances and angle into in order to calculate a speed. Let's use this equation and compare it to our analysis:
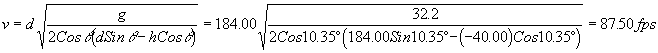
We see that the results are the same.
Next, we will examine the case if we had not known the third point in this airborne trajectory. In that case, we would have been forced to assume a take off angle for a minimum speed. That calculation follows.
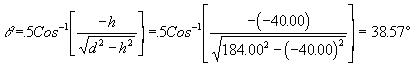
Substituting this angle into the airborne equation, we find:
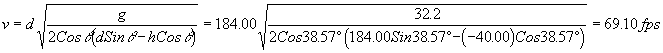 or 47 mph.
or 47 mph.
Notice that there is a difference of 12.55 mph between the unknown take off angle minimum speed estimate and the three-point airborne speed estimate method.
Conclusion
This paper introduced a treatment for an airborne trajectory analysis when three points along the airborne path are known. Use of this method eliminates the need for estimating a take off angle. Estimating a take off angle can result in significantly underestimating an airborne speed.
After studying this paper, the reader should be able to apply this approach to any three point airborne trajectory. For those that found this treatment a difficult read, a review of the derivative and systems of equations is recommended.
Acknowledgement
I wish to give special thanks and appreciation to Professor Josh Guttman of Bergen Community College, NJ, for the time he spent reviewing this paper, and the many hours of enjoyment and knowledge I gained as a student in his physics class.
|
Copyright ©
|