
The Traffic Accident Reconstruction Origin -Article-


The Traffic Accident Reconstruction Origin -Article-
|

|
Introduction
This article begins with a discussion of the methods that may be used to solve second-degree equations, including the quadratic equation. The information is used as a foundation for the discussion of systems of equations. This knowledge is then applied to the conservation of linear momentum and the conservation of energy, in order to solve collinear momentum problems where none of the impact velocities are known. These procedures are by no means new; they are perhaps as old as algebra itself, and have been used by reconstructionists in the past. It is the intent of this article to give those who have not been exposed to the topic before, a firm background in what can be a tedious subject.
Second-Degree Equations
The most common type of second degree equation we encounter as reconstructionists
are those that have a variable that is raised to the second power, such as
![]() in
in
![]() . A simple second-degree equation is
. A simple second-degree equation is
![]() . We can solve this equation easily by taking the square
root of both sides:
. We can solve this equation easily by taking the square
root of both sides: ![]() . Therefore,
. Therefore,
![]() , since both
, since both ![]() and
and
![]() . This method of solving a second-degree equation is known
as the square root method. Another way we could have solved this equation is with the
factoring method.
. This method of solving a second-degree equation is known
as the square root method. Another way we could have solved this equation is with the
factoring method.
|
Our original equation |
|
|
Subtract 9 from both sides of the equation |
|
|
|
|
|
Find the numbers that will make the left side of the equation equal 0. |
|
Just like taking the square root of both sides, our answer is ![]() .
.
While the square root method is easier, consider the equation ![]() . Here, we just can't take the square root of both sides. Nor can we just divide both sides by
. Here, we just can't take the square root of both sides. Nor can we just divide both sides by
![]() to get
to get ![]() . While 2 is part of the solution, it is not the complete solution. We proceed as follows:
. While 2 is part of the solution, it is not the complete solution. We proceed as follows:
|
Our equation |
|
|
Subtract |
|
|
Factor out |
|
|
Find the numbers that will make the left side of the equation equal 0. |
|
Thus, the solutions to ![]() are 0 and 2. Check the
solutions: substitute 2 for x in the original equation and see if it satisfies the equation. Do the same for 0. Notice that a second-degree equation
gives us two solutions. How about
are 0 and 2. Check the
solutions: substitute 2 for x in the original equation and see if it satisfies the equation. Do the same for 0. Notice that a second-degree equation
gives us two solutions. How about ![]() ? The square root method will not work. We can factor this equation, though, into
? The square root method will not work. We can factor this equation, though, into ![]() . This is done by finding two numbers whose product
is the third term (15), and whose sum is the coefficient of the middle term (8). The two numbers are 3 and 5. Once factored, it is easy to see our solution set is -3 and -5. Check this one too: substitute -3 into the original equation and see if it
satisfies the equation. Do the same for -5.
. This is done by finding two numbers whose product
is the third term (15), and whose sum is the coefficient of the middle term (8). The two numbers are 3 and 5. Once factored, it is easy to see our solution set is -3 and -5. Check this one too: substitute -3 into the original equation and see if it
satisfies the equation. Do the same for -5.
So far, we have looked at the easy ones. How about an equation such as ![]() ? We cannot take the square root of both sides, nor can we factor. We
can, however, use the quadratic equation.
? We cannot take the square root of both sides, nor can we factor. We
can, however, use the quadratic equation.
The quadratic equation is: ![]() .
.
To use the quadratic equation, we must write our second-degree equation in standard form; that is, from
the second power, to the zero power. The standard form is written
![]() . Since
. Since ![]() , and
, and ![]() , we can simplify this to
, we can simplify this to ![]() . Let's use our previous example,
. Let's use our previous example,
![]() , to demonstrate the quadratic equation. First, we see that the equation is already in standard form. Therefore, our A, B and C coefficients are 1, 1 and -5, respectively. Substitute these numbers into the quadrat
ic equation:
, to demonstrate the quadratic equation. First, we see that the equation is already in standard form. Therefore, our A, B and C coefficients are 1, 1 and -5, respectively. Substitute these numbers into the quadrat
ic equation:
|
Substitute the coefficients into the quadratic equation. |
|
|
Complete the exponent and multiplications |
|
|
This is the answer (it is acceptable to leave the answer in this form because |
|
Although factoring and the square root method are the easiest to use, they do not work for all second-degree equations. The quadratic equation will work in all cases, so it is best to know this method.
Systems of Equations
Let's look at a situation where a system of equations may be applied. You are asked to calculate the velocity of two cars given the following information:
One equation will not solve this problem for us. The most obvious equation that we can apply here comes from information that vehicle 1 is traveling 40 mph faster than vehicle 2. To show this algebraically, we write the equation
![]() (Equation A). We can see that there are an infinite number of solutions to this equation: 80=40+40, 70=30+40, 100=60+40, etc. We obviously need more information to solve this problem; this information is pr
ovided
by the first two clues. Recall that distance = velocity X time, or
(Equation A). We can see that there are an infinite number of solutions to this equation: 80=40+40, 70=30+40, 100=60+40, etc. We obviously need more information to solve this problem; this information is pr
ovided
by the first two clues. Recall that distance = velocity X time, or ![]() . When we picture in our minds the two cars, we know that they will meet after 4 hours. We also know that because vehicle 1 is traveling faster
than vehicle 2, it will cover more distance during this time. We can say with certainty that the distance vehicle 1 travels plus the distance vehicle two travels will equal 480 miles. Written algebraically,
. When we picture in our minds the two cars, we know that they will meet after 4 hours. We also know that because vehicle 1 is traveling faster
than vehicle 2, it will cover more distance during this time. We can say with certainty that the distance vehicle 1 travels plus the distance vehicle two travels will equal 480 miles. Written algebraically, ![]() . We
know that
. We
know that ![]() , so let's substitute
, so let's substitute ![]() for
for ![]() :
: ![]() . Since they both start at the same time, and mee
t
at the same time, the time for both vehicles is the same in our equation. Before proceeding further, factor the
. Since they both start at the same time, and mee
t
at the same time, the time for both vehicles is the same in our equation. Before proceeding further, factor the ![]() in the right side of the equation:
in the right side of the equation: ![]() (Equation B). Eve
n
this equation, by itself, does not help us since there are infinite solutions. Let's call on Equation A to give us a hand. We will substitute equation A --solved for
(Equation B). Eve
n
this equation, by itself, does not help us since there are infinite solutions. Let's call on Equation A to give us a hand. We will substitute equation A --solved for ![]() --into Equation B. When we do this, we have an
equation that looks like this:
--into Equation B. When we do this, we have an
equation that looks like this: ![]() . The time in this case is 4 hours; therefore, we substitute 4 for t giving
. The time in this case is 4 hours; therefore, we substitute 4 for t giving ![]() . Now we have an equation we can solve because it only has on
e variable:
. Now we have an equation we can solve because it only has on
e variable:
|
Our original equation. |
|
|
Combine like-terms. |
|
|
Distribute the 4 to the right side. |
|
|
Subtract 160 from both sides. |
|
|
Divide both sides by 8. |
|
This equation tells us that vehicle 2 was traveling at 40 mph. To calculate vehicle one's velocity, we substitute vehicles two's velocity into equation A, which was ![]() . Therefore,
. Therefore,
![]() . Vehicle 1 was traveling 80 mph.
. Vehicle 1 was traveling 80 mph.
Let's look at one more example before we apply this to accident reconstruction. How can we find the dimensions of a rectangle, knowing that its area is 50 square inches and its perimeter is 30 inches? Our first equation is that for area
,
length times width (![]() ). In this case, we know the area is 50 square inches, so
). In this case, we know the area is 50 square inches, so ![]() . Our second equation deals with the perimeter; that is,
. Our second equation deals with the perimeter; that is,
![]() . Since we know that the perimeter is 30 inches,
. Since we know that the perimeter is 30 inches,![]() . Let's simplify this last equation by dividing both sides, right now, by 2 (It is not necessary to perform this step, but
doing so will make the math easier).
This gives us
. Let's simplify this last equation by dividing both sides, right now, by 2 (It is not necessary to perform this step, but
doing so will make the math easier).
This gives us![]() . As with the first example, both equations,
. As with the first example, both equations, ![]() and
and ![]() , have an infinite number of solutions. But also similar to the
first example, we have two unknowns (l and w) and two equations. Solving for
, have an infinite number of solutions. But also similar to the
first example, we have two unknowns (l and w) and two equations. Solving for ![]() in the second equation gives us
in the second equation gives us ![]() . One word here before we proceed: we can just as easily solve
for
. One word here before we proceed: we can just as easily solve
for ![]() or
or ![]() , and in either equation. Now we substitute
, and in either equation. Now we substitute ![]() for
for ![]() , in the first equation:
, in the first equation:
![]() . From here, we solve the equation algebraically. Distribute the
. From here, we solve the equation algebraically. Distribute the ![]() in the right side of the equation to get
in the right side of the equation to get ![]() At this point we must r
ecognize
that our equation is second degree because w is squared. This tells us that we can use the quadratic equation,
At this point we must r
ecognize
that our equation is second degree because w is squared. This tells us that we can use the quadratic equation, ![]() , to solve our equation. First, we must put our equation into standard form. In this case we get,
, to solve our equation. First, we must put our equation into standard form. In this case we get,
![]() . Now we substitute our values into the quadratic equation and solve:
. Now we substitute our values into the quadratic equation and solve:
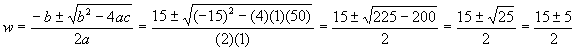
![]()
![]()
Note that the quadratic equation will always yield two answers. Which answer is
correct? Mathematically speaking, they are both correct. Conceptually however, only one answer is correct.
In real-world applications, we need to apply some reasoning to the solutions. If we accept that the width is 10, then the length, by the second equation, would be ![]() or
or ![]() =5. Th
is would be a rectangle whose width is longer than its length. Our definitions of length and width specify that the length of an object is its longest
side; therefore, because of our definitions --and only because of our definitions --we reject this solution. When we try 5 for the width, then our length would be 15-5=10. This makes sense for our definitions of length and width. Is our solution correct?
Substituting 5 for
=5. Th
is would be a rectangle whose width is longer than its length. Our definitions of length and width specify that the length of an object is its longest
side; therefore, because of our definitions --and only because of our definitions --we reject this solution. When we try 5 for the width, then our length would be 15-5=10. This makes sense for our definitions of length and width. Is our solution correct?
Substituting 5 for ![]() , and 10 for
, and 10 for ![]() into our original equations shows us that the area would be 50 square inches (10)(5), while the perimeter would be 30 inches
into our original equations shows us that the area would be 50 square inches (10)(5), while the perimeter would be 30 inches![]() . Therefore, we have found the correct solution to our problem.
. Therefore, we have found the correct solution to our problem.
At this point, the reader should recognize that when we are presented with two unknown variables in an equation, we have an infinite number of solutions. However, if we have at our disposal two independent equations that describe the sa me two unknown variables, we are able, through substitution, to solve the system of equations. Other methods for solving a system of equations exist, but we will leave that for some other time.
Case Study #1
How can second-degree and systems of equations assist us with accident reconstruction? Imagine you are called to reconstruct a serious collision in which vehicle 1 strikes vehicle 2 in the rear. There is 100% overlap. The driver of vehicle 1 states that vehicle 2 was stopped on the highway. The driver of vehicle 2 states he was not stopped; in fact, he states he was traveling at the speed limit when vehicle 1 approached at a very high rate of speed and then struck his car. There are no witnesses to corroborate either of the driver's statements, and there is no physical evidence to suggest whether vehicle 2 was stopped or in motion. The only evidence available at the scene is distinct post-collision tiremarks from both vehicles, and roadway gouging that indicates the area of maximum engagement. Crush measurements were taken from both of these vehicles. From these crush measurements, an estimate of the energy dissipated damaging both vehicles is made. The following table depicts the only available information regarding this collision:
|
|
Vehicle 1 |
Vehicle 2 |
|
Mass |
90 Slugs* (2898 lbs) |
60 Slugs (1932 lbs) |
|
Post Impact Velocity |
30 fps (20.4 mph) |
30 fps (20.4 mph) |
|
Energy dissipated damaging both vehicles |
45,000 ft-lbs |
|
(For a short discussion on mass, weight and slugs see Appendix A)
We will first look at this from the momentum aspect (we will assume there is no restitution, and both vehicles stayed together after impact). The equation for collinear momentum is ![]() . Because
the post impact velocities of both vehicles are the same, we rewrite the equation as
. Because
the post impact velocities of both vehicles are the same, we rewrite the equation as ![]() . We substitute the information we know into the equation to get
. We substitute the information we know into the equation to get ![]() . Complete the
operations indicated in the right side of the equation to give us equation 1:
. Complete the
operations indicated in the right side of the equation to give us equation 1:
|
Equation 1 |
|
This should look familiar by now. We have an equation with two unknown variables; we need another independent equation to solve the system of equations. Our obvious choice is the conservation of energy. For this example, we will use the following equation:
|
Energy Before The Collision |
= |
Energy Dissipated |
|
Energy of V1 + Energy of V2 |
= |
Energy of V1 + Energy of V2 + Energy spent damaging both vehicles |
|
|
= |
|
Let's do some factoring and substitution before we proceed:
|
Our original equation |
|
|
|
Multiply both sides by 2 |
|
|
|
Factor out the post velocities, which are the same for this collision. |
|
|
|
Substitute known values |
|
|
|
Perform operations in the parentheses. |
|
|
|
Complete remaining operations (Equation 2) |
|
|
Now we have a second equation to complete a system of equations. Before we do this, we must rearrange one of the equations for substitution into the other, by explicitly solving for one variable. We will do this with equation one, becau
se
as a first-degree equation it will be easier. We now arbitrarily choose which variable to solve for;
we will solve for![]() .
.
|
Equation 1 |
|
|
Subtract |
|
|
Divide both sides by 60 (Equation 3) |
|
We now substitute equation 3 into equation 2:
|
Our new equation with only one variable |
|
|
Square the binomial in the left side. (See Appendix B for a short discussion on squaring a binomial.) |
|
|
Distribute 60 |
|
|
Combine like terms |
|
|
Arrange the equation in standard form |
|
We can tell immediately that we can't use the square root method of solving this equation; and I don't recommend wasting time trying to factor (although it can be done in this case). We will go directly to the quadratic equation to solve for vehicle one's impact velocity.
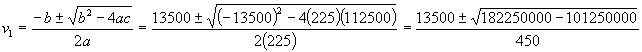
![]()
Like all second-degree equations, we have two answers that are mathematically correct. But which one is conceptually correct? Before we answer this, let's calculate vehicle two's velocity using equation 3, and present the solutions in tabular form.
|
When Vehicle 1's velocity is |
Vehicle 2's velocity is |
|
|
Solution 1 |
50 fps |
0 fps |
|
Solution 2 |
10 fps |
60 fps |
Solution 2 must be eliminated. Remember that this is a rear-end collision, in which vehicle 1 strikes vehicle 2 in the rear. Solution 2 has vehicle 2 going faster than vehicle 1. If this were the case, the collision never occurs. Therefore, solution one is correct, and we can concur with driver one's statement that vehicle 2 was stopped on the highway. It should be noted that solution two could, in fact, be a real collision involving the same momentum, and dissipating the same energy as solution 1. The roles are reversed, however, with vehicle 2 striking vehicle 1.
Case Study #2
The last application this article will discuss is a collinear head-on collision. The following diagram will be used for this discussion:
|
|
|||
|
Mass |
90 Slugs* (2898 lbs) |
60 Slugs (1932 lbs) |
|
|
Post-impact velocity |
14 fps east |
14 fps east |
|
|
Energy dissipated doing damage |
145800 ft-lbs |
||
In this collision, eastbound vehicle 1 strikes westbound vehicle 2 with 100% overlap. After the collision, both vehicles move off eastbound together, at 14 fps. As with Case Study #1, you are unable to estimate an impact speed for one of the vehicles. The only additional information you have comes from the crush measurements of both vehicles. From these crush measurements, an estimate of the energy dissipated damaging both vehicles is made. Your job is to calculate the impact speeds of both vehicles, knowing only the data given in the diagram. As with the rear-end collision, let's st art by looking at the momentum for this collision (assume no restitution, and both vehicles stayed together after impact).
|
The momentum equation |
|
|
Rewrite because both post velocities are the same. |
|
|
Substitute our known values. |
|
|
Complete the operations on the right side. |
|
|
Equation 4 |
|
As we have seen before, we have an equation with two unknown variables. We will use the conservation of energy, again, for our second equation.
|
Our original equation. |
|
|
Multiply both sides by 2. |
|
|
Factor out the post velocities, which are the same. |
|
|
Substitute known values. |
|
|
Calculate right side. (Equation 5) |
|
Now we need to solve for ![]() or
or ![]() in either equation 4 or 5. We will use equation 4 because as a first-degree equation, it is easier to solve. We must also
decide which variable to solve for. As with our prior example, it does not make a difference which one we choose. Manipulating equation 4 to solve for
in either equation 4 or 5. We will use equation 4 because as a first-degree equation, it is easier to solve. We must also
decide which variable to solve for. As with our prior example, it does not make a difference which one we choose. Manipulating equation 4 to solve for ![]() gives us equation 6.
gives us equation 6.
|
Equation 4 |
|
|
Equation 6 |
|
We now substitute equation 6 into equation 5.
|
Equation 5 |
|
|
Make the substitution |
|
|
Square the binomial in the left side*. |
|
|
Distribute 60 in the left side. |
|
|
Combine like terms. |
|
|
Arrange the equation in standard form. |
|
We will go right to the quadratic equation to solve for ![]() .
.
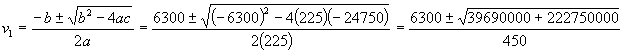
![]()
Our two possible answers are 50 and -22 fps. Before we can determine which answer is correct, we need to use equation 6 to solve for ![]() . When we do so, we find the following relationships:
. When we do so, we find the following relationships:
|
When Vehicle 1's velocity is |
Vehicle 2's velocity is |
|
|
Solution 1 |
50 fps |
-40 fps |
|
Solution 2 |
-22 fps |
68 fps |
At first, both answers appear to be possible, because we have one vehicle traveling in each direction. Let's refer back to the diagram for this collision and consider the momentum aspects.
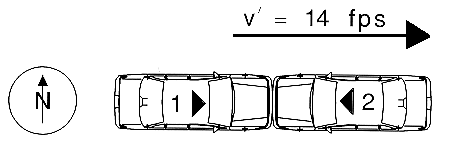
|
Mass X Velocity = Momentum |
Mass X Velocity = Momentum |
Direction of travel after impact |
|||||
|
Solution 1 |
90 slugs |
50 fps |
4500 slug-fps |
60 slugs |
-40 fps |
-2400 slug-fps |
east |
|
Solution 2 |
90 slugs |
-22 fps |
-1980 slug-fps |
60 slugs |
68 fps |
4080 slug-fps |
west |
What we are interested in looking at is the magnitude of momentum for each vehicle. We do this by considering the absolute value of the reported momentum. Recall that in collinear momentum the sign of the momentum value indicates direction only. When we consider the momentum magnitude for solution 2, we see that vehicle 2 has mo re momentum than vehicle 1; therefore, after the collision, both vehicles would have moved west. This is not what occurred in the actual accident, so we must disregard solution 2 --it is not conceptually correct. In solution 1, however, it is reported that vehicle 1 has more momentum. Therefore, after the collision, we would expect both vehicles to move east. Because this is what actually occurred, we accept this solution. As we saw with case study #1, solution 2 can be an actual collision involving the same momentum and dissipation of energy. However, each vehicle would have approached from the opposite direction and at different speeds. Notice that t he closing velocities for both solutions are the same (90 fps). We are only able to reject solution 2 because it does not correspond with the evidence at the scene.
Conclusion
This article described only a few applications where systems of equations and second-degree equations may be applied to accident reconstruction. Systems of equations may be applied to collisions that are not collinear, as well as other disciplines of accident reconstruction. It should be observed that these two mathematical concepts are not dependent upon each other. You do not necessarily need two equations to solve a second-degree equation, and you do not necessarily need a second-degree equation to solve a system of equations.
This article also made some assumptions about the sample collisions presented: it was assumed that momentum and energy analysis was appropriate. As with any case the reader reconstructs, it is important that the equation(s) and/or procedures he utilizes fit the basic physics model from which the equation was derived. In this article, it was assumed that momentum and energy analysis (via crush measurements) were appropriate for the collisions we studied. The reader is cautioned to consult other resources about these topics before proceeding with a momentum and/or energy analysis.
Appendix A a short discussion on weight and mass.
Appendix B expanding a binomial.
Andrew Rich is a sergeant with the Palisades Interstate Parkway Police where he is commanding officer of the Accident Investigation Unit. His other assignments include: on-call-investigator for the Bergen County Prosecutor's Office Fatal Accident Investigation Unit, commanding officer of the Search and Rescue Unit, and programming his department's database application systems.
Palisades Interstate Parkway Police
P.O. Box 155
Alpine, NJ 07620
(201) 768-6001
or via Email: [email protected]
|
Copyright ©
|