
The Traffic Accident Reconstruction Origin -Article-


The Traffic Accident Reconstruction Origin -Article-
|

|
Error Analysis for Drag Sleds Method 2- A Drag Sled Drag sled convention recommends multiple pulls across the surface in question. Once
ten readings are taken. Those results are averaged to find the value of drag factor.
The following data was obtained in a drag sled test on a paved surface. Time: 9:50 AM, Date 6/6/86, sled weight: 54 pound sled, Scale: Hanson Model 8920,
Number of Samples: 10 (Drag sled test conducted by J.F. (Jim) Mitchell
[email protected]) Pull Data (pounds)
|
42 |
40 |
40 |
38 |
38 |
40 |
42 |
38 |
40 |
41 |
We will use the following Equation to determine uncertainty:
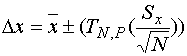 Equation 1
Equation 1
Where,
![]() = 39.9 - The average
(mean) of the tests
= 39.9 - The average
(mean) of the tests
![]() = 1.52 - The Standard
Deviation of the tests
= 1.52 - The Standard
Deviation of the tests
![]() = 10 - The Number of
tests in the sample
= 10 - The Number of
tests in the sample
![]() = 2.26 -
The t estimator from the table with 10 samples at 95%
probability
= 2.26 -
The t estimator from the table with 10 samples at 95%
probability
![]() = 1.08 Our answer
for uncertainty- The range in which the actual value of x lies at the given probability.
Where:
= 1.08 Our answer
for uncertainty- The range in which the actual value of x lies at the given probability.
Where:
We must also find the uncertainty in the value of weight of the drag sled. We will assume the scale to be calibrated. We will also assume that we are able to read to half the values incremented on the scales index. The scale is indexed every 2 pounds, so the resulting uncertainty is 1 pound.
Next, we must examine how these uncertainties propagate through the equation to drag factor.
The Equation for drag factor from a drag sled is
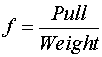
Uncertainty propagates to the measured value through the partial derivatives of this equation. Those partial derivatives are
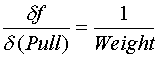
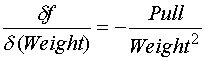
Using the Average value for Pull calculated above as 39.9 lbs. and Weight of the sled as 54 lbs. yields the following sensitivities.
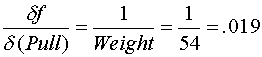
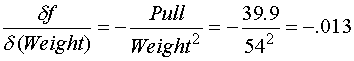
Using the uncertainty value for Pull calculated above as 1.09, and an uncertainty of 1(half the scale's incremented value) for Weight yields the following for uncertainty propagated to the calculated drag factor.
Uncertainty in pull propagated to drag factor is
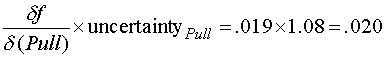
Uncertainty in Weight propagated to drag factor is
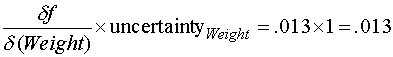
And finally, the total uncertainty in drag factor is the sum of these two values or .02+.013=.033
So, we can express the results of this drag sled test as follows: There is a 95% probability that the true value of the drag factor is .74 +- .033.
|
Copyright ©
|