
The Traffic Accident Reconstruction Origin -Article-


The Traffic Accident Reconstruction Origin -Article-
|

|
The Use of Mathcad for Calculations Rafal Szczypinski Abstract A traffic accident reconstruction expert must make many calculations when
analyzing a collision. A calculator can be very useful in this regard. A computer
program especially designed for traffic accident analysis offers some advantages over
the calculator. Calculators require the expert understand each step in a calculation.
Accident reconstruction computer programs allow the expert to determine solutions without
necessarily understanding each all teh steps in the process. The fear of course is garbage in-
garbage out. Computer based calculators offer the best of both worlds. Like a computer program
they are very fast at performing calculations. But like a calculator they require that
the user understand each step. Mathematica ©, MATLAB and Mathcad are three
such programs. This article will focus on the use of Mathcad by MathSoft®.
It will also be helpful for those who have programs like Mathcad, but are unfamiliar
with applications in the field of traffic accident reconstruction. 1.Introduction The analysis of a traffic accident can require many calculations. A large number
of these accidents fall into categories where the solutions are realized with the same
or similar algorithms. This of course is why accident reconstruction computer programs
can be produced. It is my opinion that the first step in becoming an expert is to learn and understand
the mathematical and physical basis of an accident. Then use this information for the
analysis. A program that "hides" all its calculations and shows only inputs and outputs
should be used only after the underlying basis is known. So, the first step should be to calculate an accident "manually" and learn the method
of analysis. Manually need not mean pencil in hand. The calculations are hard enough and �
as I said � often similar. The best idea is to use a computer application that shows all
steps of a solution but could be used for other solutions in similar accidents. This is
exactly what Mathcad does. 2. What is Mathcad? Mathcad is general-purpose mathematical application for calculations. It has many
basic and advanced built-in functions like trigonometric, hyperbolic, exponential,
logarithmic, complex, conditionals and others. It can integrate, differentiate, and
solve equations � on stated values as well as symbolic values. Most
importantly, this is done in conventional notation instead of some program specific syntax. Mathcad can do everything that an expert wants and needs. A very important feature is the
notation. Mathcad's template is similar to natural notation, so the solutions are clear and
easy to read for "common people". I frequently say: calculations made with Mathcad are like
solution in a student's exercise book � First data, next formulas (with some comments) and
finally a solution � the value(s), diagram(s) and so on. General Program Flow Each Mathcad Template has three basic parts. A simple example of a freely falling
object follows: Part 1- Establishing the values Part 2

Part 3
- Specifying the output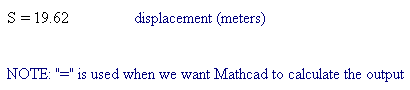
Notice that each calculation or operation can be explained in a text box beside it. Adding text descriptions are not necessary but add greatly to the understanding of the template. Notice also that Mathcad performed the calculation symbolically taking the givens in Step 1 and performing the calculation in step 2. The result is output in Step 3. This simple output statement in step 3 could have just as easily been a table of displacements or a graph. Now on to some examples.
Example 1
I have prepared the solution of the motion formula of a vehicle as an example of Mathcad's basic possibilities that are useful in a field of accident reconstruction. The one-dimensional model of Newton's second law for the slowing of a vehicle (without engine braking) would appear like:
(1) 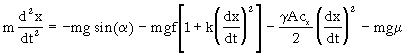 ;
;
where: m - mass of a vehicle, x - distance, t - time, g - gravity acceleration, a - road slope, f - rolling friction coefficient, k - f change coefficient (f dependence on velocity), g - air density, A - effective vehicle front surface, cx - aerodynamic drag coefficient, m - friction coefficient. The analytic solution of this differential equation is rather difficult.
The simple way to find the solution of the common differential equation:
(2) 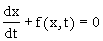
is numerical integration with the Euler method. The basis for this method is to approximate the solution for all variables between xn and xn+1 with the solution for xn like:
(3) 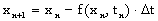
The solution to equation (1) consists of presenting this equation as a recurrent formula, like (3). In Mathcad it appears as follows (it is part of the template named vehicle.mcd included to this article):
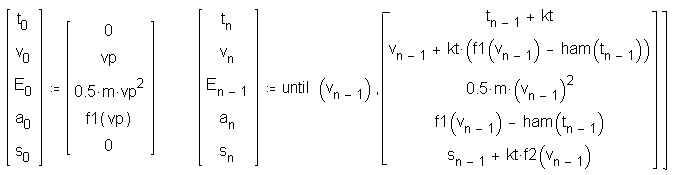
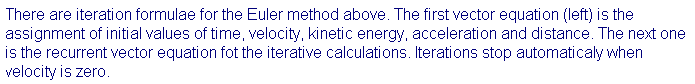
Solutions for distance, speed, acceleration, and kinetic energy are presented in diagrams on the template. As an example Figure 1, included below, is the diagram for acceleration (deceleration in fact - note the change after the first second - this is the decreasing influence of aerodynamic and rolling drag):
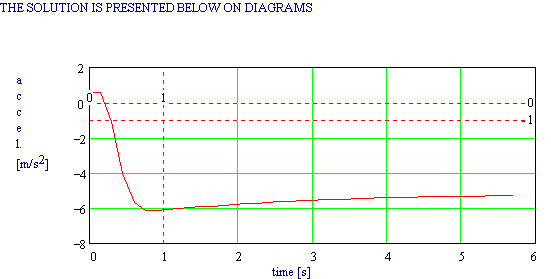
Figure 1
3. How to use Mathcad?
The general approach is to prepare templates for the calculations of many types of accidents (sometimes with several variants). For example, pedestrian impacts by a skidding vehicle, impacts with a tree or post after skidding, car to car collisions, and so on. Each of these types of accidents is calculated in similar way. So if I have to analyze an impact with a tree once, the next impact with a tree will be similar. If I have a method for one pedestrian impact I can calculate the next one in a similar way. Of course each event must be considered individually but the basic calculation method, and template, will be similar.
Example 2
For example, an accident with an impact into a tree might occur like this: a vehicle is braked (skidding), it impacts the tree and rebounds to rest. The vehicle loses its kinetic energy during each phase of the event. Each loss can be evaluated and the sum will represent the initial velocity of the vehicle as illustrated below (this is a portion of the tree.mcd template):
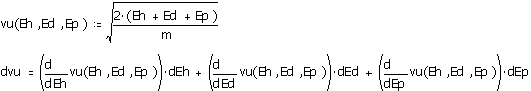
Figure 2
Figure 2 above is a portion of Mathcad's template for this problem. Here vu is initial speed, Eh - energy loss during braking, Ed - energy loss on impact, Ep - energy loss during post-impact motion. The second row is an error calculation with total differential method. The particular derrivatives (dEh, dEd, dEp) are successively calculated in the template. It is worth noting how the differential as seen in the second row of illustration is calculated. Mathcad can calculate the derivative (in place and symbolically), so I can instruct Mathcad to: "calculate the derivative of defined function F(x) on variable x (with specific value)" and I do not care how Mathcad calculates it (This is not quite true, but it is close enough). As a solution to such calculations I get the value of the initial velocity and calculated deviation, so the true solution is a range of velocities which accounts for the uncertainty.
Example 3
The next example is collision with pedestrian. Let us imagine that a person walks across a street in front of approaching car. The driver brakes but he doesn't avoid impact. I can determine the impact point, the pedestrian's pre collision path, and the length of locked wheel tire marks before and after impact. I assume pedestrian's pre collision velocity and friction coefficient. The questions are: What was the vehicle's initial speed? What was the distance between the car and the pedestrian when the driver 'should have' recognized the hazard? How long did the emergency last? What was the collision speed? This speed and time/distance analysis will be prepared as a Mathcad template and will answer all these questions.
As with other problems of this type we will work from rest back toward the approach. The first step is to calculate the impact velocity from the length of tire marks after to collision with the energy conservation law. Next I have to account for the increasing (still working backwards) vehicle velocity as it was braked before impact. Assuming the friction coefficient I can calculate the time of vehicle deceleration before and after impact. The time before impact must be increased by the brake actuation time- when brake forces increase prior to lockup. Brake actuation times range from 0.2-0.3 sec. Now I have total time of braking before collision. If I compare this time with the time of pedestrian motion I will know where the driver's actions began. I can also calculate the distance between pedestrian trajectory and vehicle at start of the perceived dangerous situation. Finally I can draw the diagram illustrating vehicle's and pedestrian's motion. This diagram is presented below:
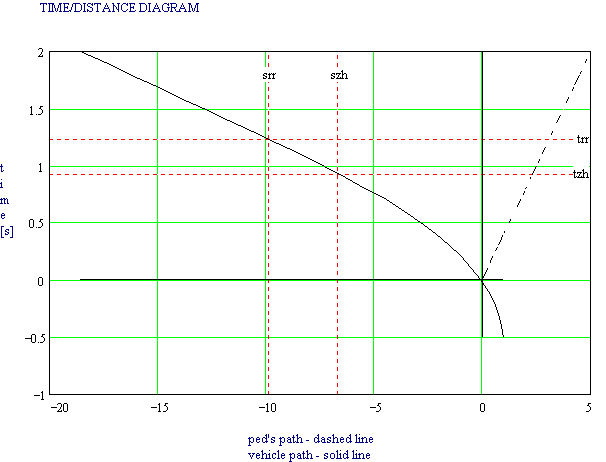
trr = Time of first contact with Brake Pedal
tzh = full brake application
srr = pedestrians location at perception
szh = pedestrians location at full brake application
This diagram is the solution to the problem presented above, the template named ped.mcd.
4. Conclusion
The goal of this article was to present computer calculators in general and Mathcad specifically as useful tools for the traffic accident Reconstructionist. It is difficult to exhibit all of the features of this powerful and complex application without writing a book. I hope that this article and the three examples linked below give a basic idea of the numerous ways these types of programs may be used.
I have found Mathcad particularly helpful when repeated calculations are necessary- for example changing estimated values that occur in a particular problem. Mathcad templates also make excelent supplements for reports as Exemplified by the illustrations in this article. All were created in Mathcad. Seeing the calculations is preferred and welcomed by juries and police.
View the entire Mathcad Templates cited above
About the Author
Rafal Szczypinski, age 33, is a police 1st lieutenant traffic accident expert at the Police Laboratory in Slupsk, north Poland. He graduated in physics (M.S.) at University of Slupsk in 1989, in traffic accident examinations and reconstruction in 1992, and the Police Experts Course at the Police Academy in Szczytno, 1995.
His work in the Laboratory is concerned with: vehicle examination to find the influence of vehicle defects on accident causes; vehicle lamps to state which lamps were on during the accident; pedestrian shoes to state his position relative to the vehicle at impact; and general accident cause analysis and reconstruction.
He is a native Polish speaker and has written this article in English with limited editorial assistance.
The author offers his experience with anyone that is interested in using Mathcad.
He can be reached at [email protected]
|
Copyright ©
|