
The Traffic Accident Reconstruction Origin -Approach Angles Problem-


The Traffic Accident Reconstruction Origin -Approach Angles Problem-
|

|
The Falling Pedestrian (more correctly The Toppling
Pedestrian
by Dr. Eddie Baart
This problem was posted in TARO's Approach Angles. The question resolves to the following:
Could the pedestrian have "fallen" to a position where his waist was 10 feet from the curb?
Facts
The problem states that the pedestrian fell off the curb into the roadway. The height of this curb is unspecified. This solution will include this height as a general variable h. This general approach will also allow the solution to cover similar situations where the pedestrian could have fallen from a great height.
The top of the ledge is a vertical distance of h feet from the ground. The pedestrian
was struck 10 feet horizontally from the edge of the curb. His CM is
![]() off the ground where l
is his overall height.
off the ground where l
is his overall height.
Questions
What would the pedestrian's horizontal velocity be if you assumed that his body were rigid from the feet to the CM and he tipped out away from the curb while standing on it? What would be the probable horizontal distance traveled from the edge to the point of impact?"
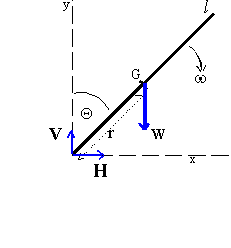
The Solution
Suppose the pedestrian is of height l (l/2 is distance from center of
gravity to his feet). We describe the motion of the center of gravity (G) in terms of
the coordinates ![]() the angle of lean and r as
shown in the diagram. The x coordinate of G is l/2 cos
the angle of lean and r as
shown in the diagram. The x coordinate of G is l/2 cos
![]() so its x component of velocity (by
differentiation) is
so its x component of velocity (by
differentiation) is
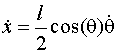 Equation.(a)
Equation.(a)
and its x component of acceleration is
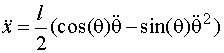 Equation(1)
Equation(1)
The two terms in the x acceleration can be recognized as the horizontal components of
the tangential acceleration ![]() and the radial
(centripetal) acceleration
and the radial
(centripetal) acceleration ![]() There is a radial
acceleration as in uniform circular motion because, although r is not
changing in magnitude, its direction is changing.
There is a radial
acceleration as in uniform circular motion because, although r is not
changing in magnitude, its direction is changing.
The feet of the pedestrian will lose contact with the ledge when the horizontal component of the force exerted on them by the ledge (H in the diagram) becomes zero i.e. when the x component of the acceleration shown above becomes zero.
In order to find the angle at which this occurs we need to find expressions for
![]() and
and ![]() .
To do this we use Newton's Second Law (for rotation) and Conservation of Energy.
.
To do this we use Newton's Second Law (for rotation) and Conservation of Energy.
Newton's Second Law
For rotational motion this law states that the moment of inertia times the angular
acceleration equals the torque (by analogy with F = ma for linear motion). The moment
of inertia of the pedestrian for an axis through his feet is
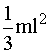
So 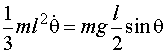 and hence
and hence
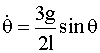 Equation(2)
Equation(2)
Conservation of Energy
![]() The rotational kinetic energy when the
pedestrian is at an angle
The rotational kinetic energy when the
pedestrian is at an angle ![]() must equal the
gravitational potential energy it has lost as his center of mass (CM) descending from its
previous height of l/2 above his feet to the new height l/2 cos
must equal the
gravitational potential energy it has lost as his center of mass (CM) descending from its
previous height of l/2 above his feet to the new height l/2 cos
![]() . Thus,
. Thus,
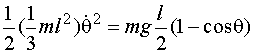
and so
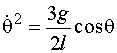 Equation(3)
Equation(3)
The Angle of Launch
We now use the condition for the horizontal force to be zero i.e. that the x acceleration of equation (1) is zero.
If we substitute equations (2) and (3) into equation (1) and set x=0 we get
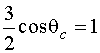 and hence
and hence
![]()
It is noteworthy to observe that this result is independent of l so it applies to the pedestrian regardless of his height, or a pencil toppling off a table.
The components of launch velocity
We can get the horizontal component of his velocity at the instant the pedestrian
leaves his feet by substituting ![]() into the
equation (3) to find
into the
equation (3) to find ![]() and then using equation
a.
and then using equation
a.
This gives 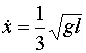 Equation(4)
Equation(4)
We can get a similar expression for the vertical speed when
![]()
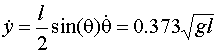 Equation(5)
Equation(5)
The Problem at Hand
We can apply equations (4) and (5) to the problem at hand. If the victim was 70 inches tall (1.778m) then l = 2 x 0.889 m (2 x 35 inches).
The height of the CM at launch is l/2 cos 48.18 above his feet = 0.593 m and vertical velocity is 1.557 m/s. So he falls 0.593m + h , where h is the curb height. If this was a normal curb of .152 m (6 inches) the victim falls 0.593 + .152 = .745 m (2.45 ft). This fall takes .39 seconds.
Since the horizontal launch velocity is 1.391 m/s (4.56 ft/s) he travels a horizontal distance of .54m (1.8 ft).
If we compare this distance to the given distance of 10 feet (3.05m), then it is obvious that this was not a simple topple with the assumptions I have used. Whether foul play occurred, I leave to your judgement.
He can be contacted at [email protected]